- Investment
- 科学论坛
-
Program
News Message
全局搜索算法
- by wittx 2021-06-25
1. 引言
全局意义上的搜索方法能够在整个可行集上开展搜索,以找到极小点。这些方法只需要计算函数目标值,不需要对目标函数进行求导。这类方法的适用面更加广阔,在某些情况下,这些方法产生的解可以作为如梯度方法、牛顿法等迭代方法的“较好”的初始点。
2. Melder-Mead 单纯形法
在此方法中引入了“单纯形”的概念,单纯形指的是在n维空间中选取n+1个点(
![[公式]](/images/download/1624587837892_95944.png) )所组成的几何形状,需要满足:
)所组成的几何形状,需要满足:![[公式]](/images/download/1624587838528_11495.png)
通俗来讲,这个条件要求在
![[公式]](/images/download/1624587838639_59032.png) 中,两个点不重合;在
中,两个点不重合;在 ![[公式]](/images/download/1624587838695_17746.png) 中,3个点不共线;在
中,3个点不共线;在 ![[公式]](/images/download/1624587838755_96499.png) 中,4个点不共面。也就是说,单纯形包围的n维空间具有有限的体积。
中,4个点不共面。也就是说,单纯形包围的n维空间具有有限的体积。2.1 基本思想
针对
![[公式]](/images/download/1624587838813_35283.png) 的最小化问题,首先需要选择n+1个点构成单纯形。具体选择方法为先选择初始点
的最小化问题,首先需要选择n+1个点构成单纯形。具体选择方法为先选择初始点 ![[公式]](/images/download/1624587838881_20478.png) ,然后在按照如下方式产生其他点:
,然后在按照如下方式产生其他点:![[公式]](/images/download/1624587838954_46999.png)
其中
![[公式]](/images/download/1624587839023_80898.png) 为空间中的标准基,
为空间中的标准基, ![[公式]](/images/download/1624587839083_76474.png) 为正数,按照优化问题的规模确定其大小。选择n+1个点之后就可以构成单纯形了。
为正数,按照优化问题的规模确定其大小。选择n+1个点之后就可以构成单纯形了。单纯形确定之后就可以通过不断迭代,使得单纯形能够朝着函数的极小点收敛。对于函数最小化的优化问题而言,目标函数值最大的点将被另外的点代替,持续迭代之后,直到单纯形收敛到目标函数的极小点。
下面具体到二维问题来说明点的替换规则。
2.2 举例:二维问题
在二维问题中,我们需要选择3个点来构成单纯形,因为需要比较对应目标函数值的大小,所以需要对每个点对应的函数值进行排序。令
![[公式]](/images/download/1624587839144_92919.png) 分别表示对应函数值最大、次大和最小的点。
分别表示对应函数值最大、次大和最小的点。在n维为中计算最好的n个点(扣除了最差的点)的重心
![[公式]](/images/download/1624587839205_77217.png) :
:![[公式]](/images/download/1624587839275_55406.png)
在二维问题中,最好点和次好点的重心为:
![[公式]](/images/download/1624587854385_32353.png)
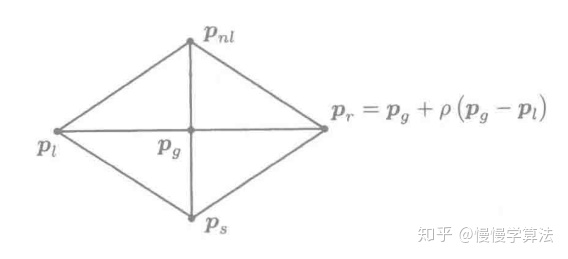
利用
![[公式]](/images/download/1624587854454_58692.png) 进行反射操作,反射系数
进行反射操作,反射系数 ![[公式]](/images/download/1624587854510_10511.png) ,在
,在 ![[公式]](/images/download/1624587854559_41136.png) 方向上对最差点
方向上对最差点 ![[公式]](/images/download/1624587854608_90884.png) 进行反射,得到反射点
进行反射,得到反射点 ![[公式]](/images/download/1624587854657_70980.png) :
:![[公式]](/images/download/1624587854706_41730.png)
然后根据
![[公式]](/images/download/1624587854785_97748.png) 的取值情况,再决定怎么取代最差点
的取值情况,再决定怎么取代最差点 ![[公式]](/images/download/1624587854856_28840.png) 。
。反射系数一般令
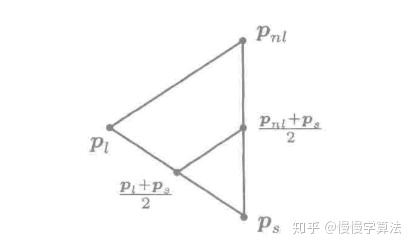
![[公式]](/images/download/1624587854907_17870.png) ,反射过程如图所示:
,反射过程如图所示:1)若
![[公式]](/images/download/1624587855259_63927.png) :
:反射出来的点对应的函数值小于原来次大的函数值,说明反射是成功的,则利用
![[公式]](/images/download/1624587855336_84334.png) 代替原来的
代替原来的 ![[公式]](/images/download/1624587855388_99426.png) 。
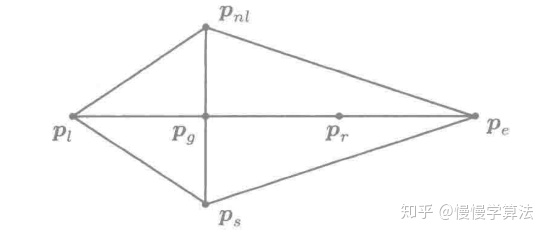
。2)若
![[公式]](/images/download/1624587855442_64814.png) :
:反射出来的点都比原来的最小值的点都要小,说明反射的太成功了,说明反射的方向很好,此时尝试再延伸,看看会不会有更好的结果:
令
![[公式]](/images/download/1624587855611_36395.png) ,其中
,其中 ![[公式]](/images/download/1624587855685_37248.png)
- 如果
![[公式]](/images/download/1624587855736_48789.png) :延伸正确,用
:延伸正确,用 ![[公式]](/images/download/1624587855805_71089.png) 代替原来的
代替原来的 ![[公式]](/images/download/1624587855896_70867.png) 。
。 - 如果
![[公式]](/images/download/1624587855947_85196.png) :延伸出来的点对应的函数值大于原来的,不能延伸了,直接用
:延伸出来的点对应的函数值大于原来的,不能延伸了,直接用 ![[公式]](/images/download/1624587856013_94679.png) 代替原来的
代替原来的 ![[公式]](/images/download/1624587856055_17342.png) 。
。
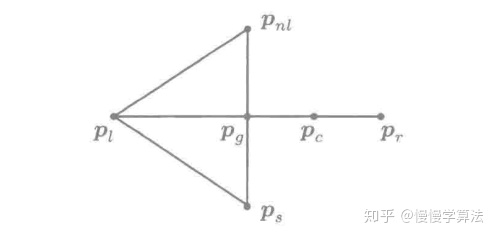
3)若
![[公式]](/images/download/1624587856100_67584.png) :
:反射出来的点对应的函数值比原来次差的点要差,此时产生两种情况,一种是比原来最差的点要更差,另一种是介于次差点和最差点中间。
- 若
![[公式]](/images/download/1624587856174_60695.png) :
:
进行外收缩,令
![[公式]](/images/download/1624587856243_86217.png) ,其中
,其中 ![[公式]](/images/download/1624587856304_89218.png) 。
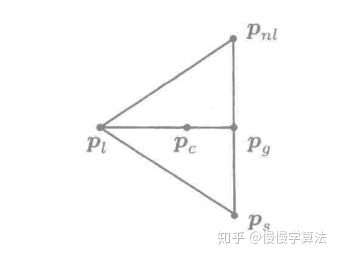
。- 若
![[公式]](/images/download/1624587856505_58358.png) :
:
反射出来的点成为了最差点,进行内收缩,令
![[公式]](/images/download/1624587856570_35940.png)
接着要对
![[公式]](/images/download/1624587856725_70161.png) 进行判断:
进行判断:![[公式]](/images/download/1624587856805_81528.png) :说明收缩以后比原来来最差点对应的值要小了,即收缩成功,用
:说明收缩以后比原来来最差点对应的值要小了,即收缩成功,用 ![[公式]](/images/download/1624587856869_12467.png) 代替
代替 ![[公式]](/images/download/1624587856933_41987.png) 。
。![[公式]](/images/download/1624587856975_17194.png) :说明收缩失败了,那就在原来的3个点中,只保留
:说明收缩失败了,那就在原来的3个点中,只保留 ![[公式]](/images/download/1624587857021_12816.png) ,
, ![[公式]](/images/download/1624587857075_28045.png) 与其它点距离减半:
与其它点距离减半:
进行这种压缩方式之后,在新的3个点中再进行上述的操作。
以上就是在二维问题中,Melder-Mead 单纯形法的搜索和迭代过程。
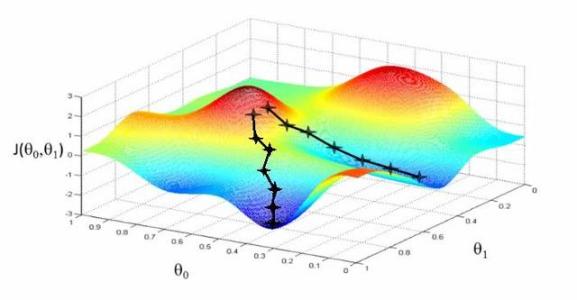
下图列举了一个利用Melder-Mead 单纯形法求救二元函数极小点的部分搜索过程:
3. 模拟退火算法
3.1 随机搜索
模拟退火法是一种随机搜索算法,随机搜索算法是一种能够在优化问题的可行集中随机采样,逐步完成搜索的方法。
![[公式]](/images/download/1624587857334_31653.png)
随机搜索方法的一个基本假设为可以从可行集
![[公式]](/images/download/1624587857417_28363.png) 中进行随机采样。通常情况下,随机选择一个
中进行随机采样。通常情况下,随机选择一个 ![[公式]](/images/download/1624587857464_81599.png) ,并在
,并在 ![[公式]](/images/download/1624587857525_67985.png) 附近在选择一个点作为下一个迭代点的备选。
附近在选择一个点作为下一个迭代点的备选。设
![[公式]](/images/download/1624587857570_85510.png) 附近可选择备选点的集合为
附近可选择备选点的集合为 ![[公式]](/images/download/1624587857616_20915.png) ,可以认为
,可以认为 ![[公式]](/images/download/1624587857667_18642.png) 为
为 ![[公式]](/images/download/1624587857752_82801.png) 的一个“邻域”。
的一个“邻域”。一种简单的随机搜索算法——朴素随机搜索算法如下所示:
1. 令
![[公式]](/images/download/1624587857800_11496.png) ,选定初始点
,选定初始点 ![[公式]](/images/download/1624587857853_16489.png)
2. 从
![[公式]](/images/download/1624587857900_68961.png) 随机选一个备选点
随机选一个备选点 ![[公式]](/images/download/1624587857957_17577.png)
3. 如果
![[公式]](/images/download/1624587858005_26803.png) ,则令
,则令 ![[公式]](/images/download/1624587858067_10799.png) ,否则令
,否则令 ![[公式]](/images/download/1624587858126_58700.png)
4. 如果满足停止规则,就停止迭代
5. 令k:=k+1,返回第2步
3.2 模拟退火法
朴素随机搜索算法的主要问题是有可能会在局部极小点附近“卡住”。如
![[公式]](/images/download/1624587858189_41258.png) 已经足够小了,如果
已经足够小了,如果 ![[公式]](/images/download/1624587858247_49650.png) 为当前的局部最小点,那么算法就无法跳出
为当前的局部最小点,那么算法就无法跳出 ![[公式]](/images/download/1624587858297_79686.png) 的范围,即陷入了局部最小的问题。
的范围,即陷入了局部最小的问题。一种解决途径是保证“领域
![[公式]](/images/download/1624587858348_74638.png) 足够大,但一旦搜索空间大了,搜索过程也会变慢,这也导致了寻找备选点的难度加大。
足够大,但一旦搜索空间大了,搜索过程也会变慢,这也导致了寻找备选点的难度加大。另一种方法是设置一种方法,让算法以一定概率接受比当前点要差的新点。这也是模拟退火的机制。
模拟退火算法:
1. 令k:=0,选定初始点
![[公式]](/images/download/1624587858399_96356.png)
2. 从
![[公式]](/images/download/1624587858455_87256.png) 随机选一个备选点
随机选一个备选点 ![[公式]](/images/download/1624587858506_71859.png)
3. 设置一枚特殊的硬币,使其在一次抛投中出现正面的概率为
![[公式]](/images/download/1624587858557_78360.png) ,在一次抛头中,如果出现正面,则令
,在一次抛头中,如果出现正面,则令 ![[公式]](/images/download/1624587858630_28730.png) ,否则
,否则 ![[公式]](/images/download/1624587858686_43697.png)
4. 如果满足停止规则,就停止迭代
5. 令k:=k+1,返回第2步
可以看出区别主要在算法第3步,这一步骤中,模拟退火法以一定概率选择选择备选点作为下一个迭代点,这一概率称为接受概率。
常用的接受概率为:
![[公式]](/images/download/1624587858739_57723.png)
exp表示指数函数,
![[公式]](/images/download/1624587858841_15177.png) 构成一组正数序列,称为温度进度表或冷却进度表。
构成一组正数序列,称为温度进度表或冷却进度表。如果
![[公式]](/images/download/1624587858894_19375.png) ,说明p=1,即始终
,说明p=1,即始终 ![[公式]](/images/download/1624587858955_68481.png) ,因为备选点的函数值已经比原来的小了,所以理应作为迭代点。
,因为备选点的函数值已经比原来的小了,所以理应作为迭代点。如果
![[公式]](/images/download/1624587859013_61480.png) ,说明这个点不好,但仍有一定概率接受这个点,这个概率为:
,说明这个点不好,但仍有一定概率接受这个点,这个概率为:![[公式]](/images/download/1624587859073_90059.png)
并且
![[公式]](/images/download/1624587859150_48145.png) 和
和 ![[公式]](/images/download/1624587859196_16144.png) 之间的差异越大,采用这个不好的点的概率就越小。类似的,
之间的差异越大,采用这个不好的点的概率就越小。类似的, ![[公式]](/images/download/1624587859277_26384.png) 越小,采用不好的点的概率也越小。
越小,采用不好的点的概率也越小。通常的做法是令
![[公式]](/images/download/1624587859323_71853.png) 单调递减至0,即模仿冷却的过程,直观的理解也就是随着迭代次数k的增加,算法趋于更差点的可能性就越小。
单调递减至0,即模仿冷却的过程,直观的理解也就是随着迭代次数k的增加,算法趋于更差点的可能性就越小。模拟退火算法中的温度必须以可可控的方式递减,具体而言,冷却过程必须足够慢,有人给出了一个合适的冷却进度表:
![[公式]](/images/download/1624587859374_32782.png)
其中,
![[公式]](/images/download/1624587859431_58268.png) 为常数,需要根据具体问题上设置。(需要足够大,以保证能够跳出局部最小点附近的区域)。
为常数,需要根据具体问题上设置。(需要足够大,以保证能够跳出局部最小点附近的区域)。4. 粒子群优化算法
粒子群算法与上述的随机搜索算法的一个主要区别是:在一次迭代中,粒子群优化算法并不是只更新单个迭代点
![[公式]](/images/download/1624587859480_69831.png) ,而是更新一群迭代点,称为群。
,而是更新一群迭代点,称为群。可以将群视为一个无需的群体,每个成员都在移动,旨在形成聚集,但移动方向是随机的。粒子群优化算法旨在模拟动物或昆虫的社会行为,如蜂群、鸟群和羚羊群的形成过程。
粒子群优化算法的基本过程为,首先随机产生一组数据点,为每一个点赋予一个速度,构成一个速度向量。点本身代表粒子所在的位置,每个点以指定的速度移动。接下来针对每个数据点计算对应的目标函数值,基于计算结果再产生一组新的数据点,赋予新的速度。
每个粒子都持续追踪其当前为止的最好位置pbest,程序也记录当前全局的最好位置gbest。
4.1 基本的粒子群优化算法
gbest版粒子群优化算法的简化版本,在每次迭代中,粒子的速度都朝着个体最好位置而和全局最好位置进行调整。
符号约定:
![[公式]](/images/download/1624587859529_32660.png) 为目标函数
为目标函数![[公式]](/images/download/1624587859577_39202.png) 表示群体的容量,共有d个粒子
表示群体的容量,共有d个粒子![[公式]](/images/download/1624587859625_31917.png) 表示粒子i的位置,对应速度为
表示粒子i的位置,对应速度为 ![[公式]](/images/download/1624587859673_25746.png) ,
, ![[公式]](/images/download/1624587859714_51420.png) 表示粒子i的pbest,
表示粒子i的pbest, ![[公式]](/images/download/1624587859766_20591.png) 表示gbest。
表示gbest。gbest版的粒子群优化算法:
1. 令k:=0,选定d个初始点
![[公式]](/images/download/1624587859824_92692.png) ,以及对应
,以及对应 ![[公式]](/images/download/1624587859883_96672.png) ,
, ![[公式]](/images/download/1624587859930_29443.png) ,
, ![[公式]](/images/download/1624587859987_13535.png) 。
。2. 对第i个粒子,随机产生两个n为向量
![[公式]](/images/download/1624587860067_46368.png) 和
和 ![[公式]](/images/download/1624587860119_76889.png) ,并从(0,1)区间内抽取随机数w、c1和c2,用于计算下一次的速度向量:
,并从(0,1)区间内抽取随机数w、c1和c2,用于计算下一次的速度向量:![[公式]](/images/download/1624587860167_10933.png)
![[公式]](/images/download/1624587860271_99149.png)
3. 针对每个新的
![[公式]](/images/download/1624587860335_60370.png) ,查看它对应的函数值,判断并更新
,查看它对应的函数值,判断并更新 ![[公式]](/images/download/1624587860397_70912.png)
4. 针对所有
![[公式]](/images/download/1624587860460_53394.png) ,查看函数值并更新
,查看函数值并更新 ![[公式]](/images/download/1624587860512_35962.png)
5. 如果满足停止条件就停止迭代,否则令k=k+1,并返回第2步。
上面
![[公式]](/images/download/1624587860560_65226.png) 表示矩阵按元素相乘得到新的矩阵,
表示矩阵按元素相乘得到新的矩阵, ![[公式]](/images/download/1624587860603_38814.png) 表示惯性系数,建议取稍微小于1的值,参数c1和c2决定了粒子趋向于“好位置”的程度,表示来自“认知”和“社会”的影响因素,即粒子本身最好位置和全局最好位置的影响,建议取值
表示惯性系数,建议取稍微小于1的值,参数c1和c2决定了粒子趋向于“好位置”的程度,表示来自“认知”和“社会”的影响因素,即粒子本身最好位置和全局最好位置的影响,建议取值 ![[公式]](/images/download/1624587860634_81202.png) 。
。4.2 粒子群算法优化的变种
粒子群算法提出以后,经过了不断地完善和修改。其中一种是收敛因子的粒子群优化算法,其更新速度的公式为:
![[公式]](/images/download/1624587860689_29195.png)
其中
![[公式]](/images/download/1624587860803_16596.png) 为收敛系数:
为收敛系数:![[公式]](/images/download/1624587860854_90942.png)
其中
![[公式]](/images/download/1624587860920_50607.png) ,收敛系数的作用在于加快收敛。
,收敛系数的作用在于加快收敛。实际应用中往往希望速度能有一个上限
![[公式]](/images/download/1624587860971_47955.png) ,之后公式里的速度更新为:
,之后公式里的速度更新为:![[公式]](/images/download/1624587861016_30446.png)
5. 遗传算法
5.1 有关术语和定义
染色体和表达模式
遗传算法并不是直接针对约束集
![[公式]](/images/download/1624587861085_49811.png) 中点进行操作,而是对这些点进行编码后进行操作。
中点进行操作,而是对这些点进行编码后进行操作。具体而言是将
![[公式]](/images/download/1624587861171_55970.png) 映射为一个字符串的集合,这些字符串是等长的,称为染色体。
映射为一个字符串的集合,这些字符串是等长的,称为染色体。每个染色体是从一个字符串集合中提取的,该集合称为字符表,如常用的二进制字符表{0,1},此时染色体就是二进制字符串。
每个染色体对应一个目标函数值,称为染色体的适应度。
字符串的长度、字符表和编码方式统称为表达模式。
一定数量的染色体构成了初始种群
![[公式]](/images/download/1624587861222_17901.png) ,之后对齐进行交叉和变异操作,在经过k次迭代之后,计算整个种群的适应度,并按照如下两个步骤构造一个新的种群
,之后对齐进行交叉和变异操作,在经过k次迭代之后,计算整个种群的适应度,并按照如下两个步骤构造一个新的种群 ![[公式]](/images/download/1624587861272_17523.png) 。
。选择和进化步骤
选择——将表现好的染色体选择出来放到另一个地方
- 轮盘赌模式
- 锦标赛模式
轮盘赌模式
选择的过程是将
![[公式]](/images/download/1624587861331_66232.png) 种群中生成
种群中生成 ![[公式]](/images/download/1624587861400_65115.png) 种群,两个种群中的染色体数量相同,都为N,这意味表现好的染色体会被重复选入M(k),每个染色体被选择的概率为:
种群,两个种群中的染色体数量相同,都为N,这意味表现好的染色体会被重复选入M(k),每个染色体被选择的概率为:![[公式]](/images/download/1624587861484_91959.png)
即个体的适应度与种群的适应度间的比值。
锦标赛模式:
从P(k)中随机选择两个染色体,比较他们的适应度,将表现好的放入M(k)中,不断进行这种操作,直到M(k)中的染色体数量为N。
进化——对M(k)中的染色体进行交叉和变异
交叉:从配对池M(k)中选择“父代”染色体,选择一个交叉点,交叉后生成“子代”,之后利用子代的染色体替代配对池中的染色体。
变异:从配对池中抽取染色体,并以一定概率随机改变其中的某个元素,产生变异。
5.2 遗产算法步骤
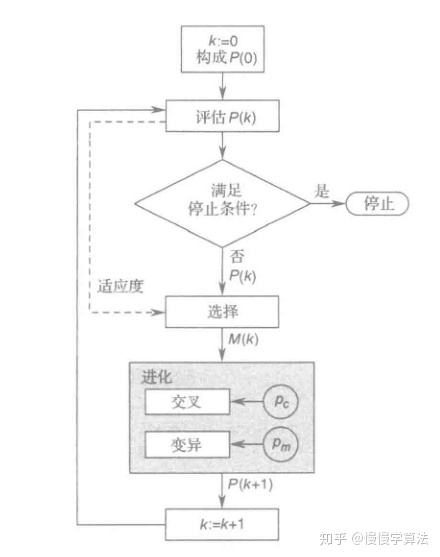
1. 令k:=0,产生一个初始种群P(0)
2. 评估P(k),即计算种群中每个个体的适应度
3. 如果满足停止条件就停止
4. 从P(k)中选择M(k)
5. 进化M(k),构成新的种群P(k+1)
6. 令k=k+1,返回到第2步
流程图如下所示:
在遗传算法的迭代过程中,持续追踪当前为止最好的染色体,即适应度最高的染色体。在一次迭代后,当前为止最好的染色体作为最优解的备选。实际上,甚至可以将其复制到新一代种群中。这是精英主义者的做法,这种精英主义的策略容易导致种群被“超级染色体”主导。但是,实际应用经验表明,精英主义的策略很多时候可以提高算法的性能。
遗传算法和其它优化算法有如下不同:
第一,不需要计算目标函数的导数(全局搜索的其他方法也有这个性质)。
第二,在每次迭代中,采用的是随机操作(与其他随机搜索方法是一致的)。
第三,每次迭代是利用一组点而不是一个点开展搜索(与粒子群优化算法相似)。
第四,对约束集进行编码,而不是直接在约束集本身上开展搜索。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=774

Best Last Month

Information industry by wittx
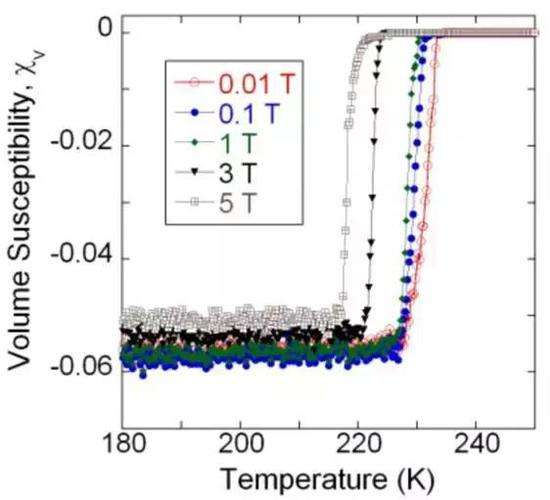
Information industry by wittx
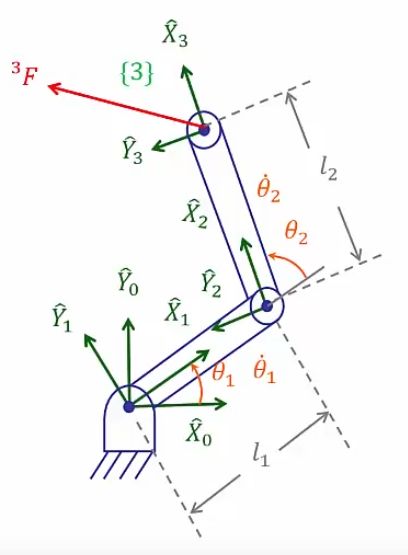
Mechanical electromechanical by wittx
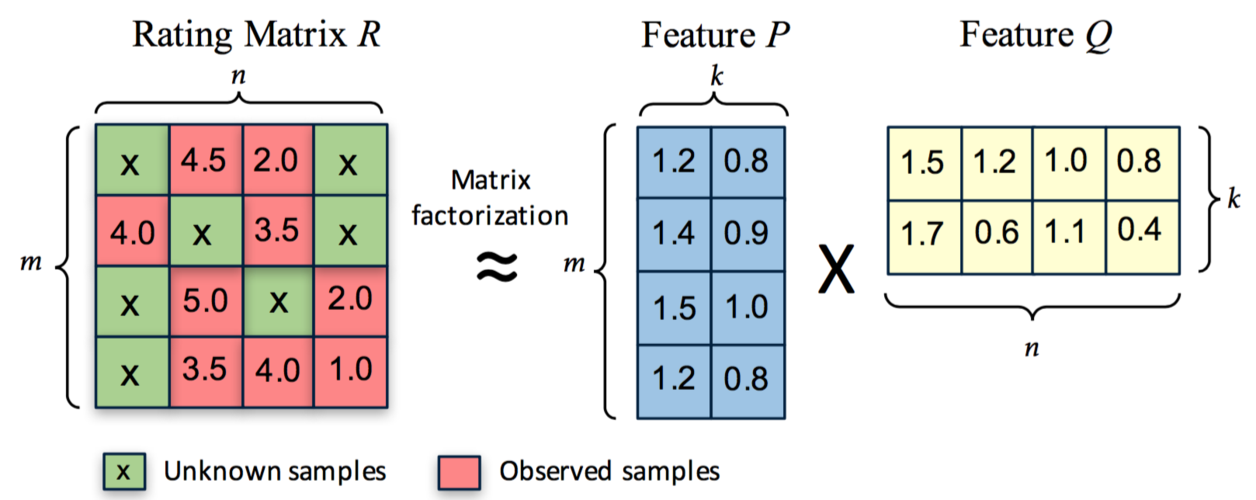
Information industry by wittx
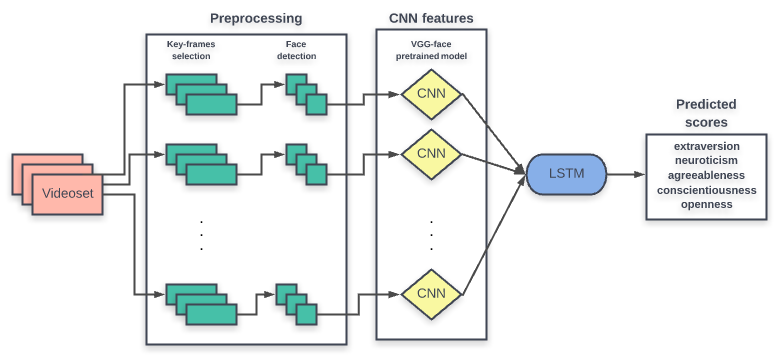
Information industry by wittx

Information industry by wittx

Information industry by wittx

Office culture and education by wittx

Information industry by wittx
Computer software and hardware by wittx