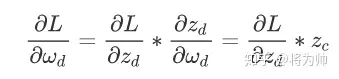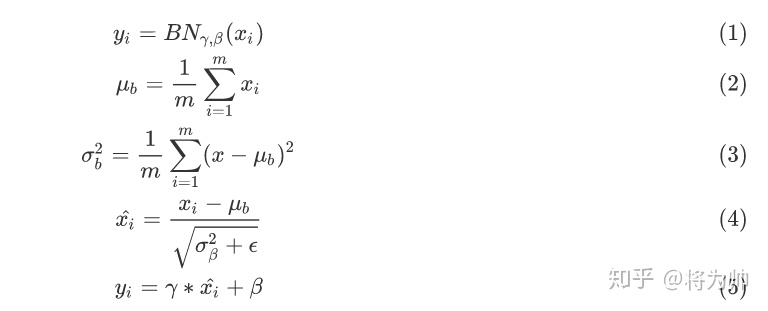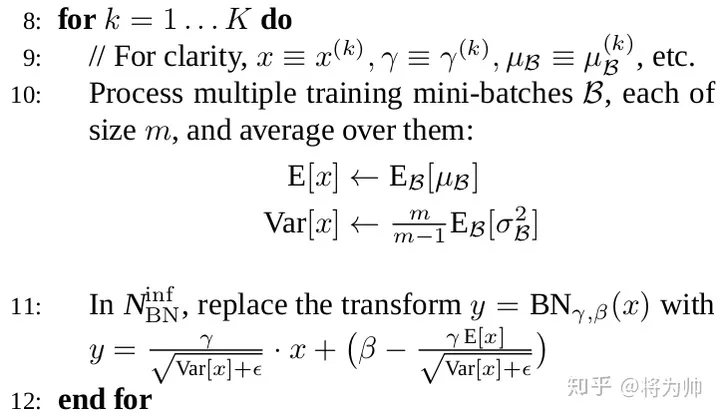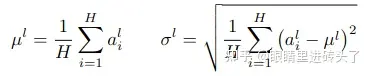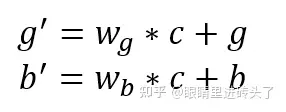- Investment
- 科学论坛
-
Program
News Message
Batch Normalization,Layer/Instance/Group Norm
- by wittx 2023-08-31
Batch Normalization逐渐成为了深度神经网络结构中相当普遍的结构,但它仍是深度学习领域最被误解的概念之一。BN真的解决了内部变量分布迁移问题ICS(Internal Covariate Shift)吗?如果没有,那么BN是如何work的?在BN基础上提出的LN(Layer Normalization),IN(Instance Normalization),GN(Group Normalization)又是什么呢?在本文中,让我们一起探索!
1. BN(Batch Normalization)解决了ICS(Internal Covariate Shift)问题?
1.1 什么是ICS(Internal Covariate Shift)?
在BN的原论文中,作者说BN解决了ICS问题,那么什么是ICS?有必要在一开始就对其有个直观通俗的解释:
ICS(Internal Covariate Shift):神经网络的中间层的输入的分布变化。
3个单词拆开理解下:"Internal"意为“内部的”,是指分布变化发生在神经网络的中间层,当然就是指神经网络的内部;"covariate"意为“协变量”,是指假设中间的的权重是我们关注的自变量,层的输出是因变量,那么层的输入可以理解为协变量;"Shift"意为变化,顾名思义,是指分布在变化。
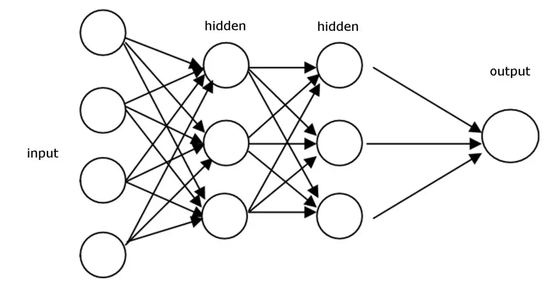
让我们试着理解下ICS是如何发生的。假设一个最简单的神经网络如下图所示:
再假设我们要优化的损失函数为L,则L相对于 d层神经元的参数w_d的偏导数的计算公式如下(链式法则),其中z_d = w_d * z_c(省略了激活函数)。根据公式可以看出:d层神经元的权重的梯度取决于上一层c层神经元的输出。
将上面得到的结论推广开来,有:
某一层神经元的权重的梯度取决于该层神经元的输入,也即取决于上层神经元的输出。
梯度之后用作反向传播以及权重的更新,该过程的重复就形成了网络的训练过程。聚焦到d层神经元上,我们使用梯度对参数作了更新后,希望新的参数会带来更小的loss,但实际可能与我们的期望不符,为什么呢?
- 第i轮迭代时,假设c层神经元的输出的分布为p_i,d层神经元的参数梯度由p_i求得,并对参数w_d作更新。
- 第i轮的梯度反向传播,对c层神经元的参数w_c也作了更新,将会导致c层的输出分布变化。
- 第i+1轮时,c层神经元的输出分布由原来的p_i变成了p(i+1)。由于第i轮时,d层神经元的参数是依据p_i更新的,分布从p_i到p(i+1)的变化,可能导致第i+1轮计算的loss不会减小。
1.2 如何解决ICS(Internal Covariate Shift)?
一种最基本的解决办法就是对网络的输入作归一化(Normalization),使得输入分布的均值为0,标准差为1。然而这个方法仅在网络不深的情况下才奏效;一旦网络是比较深的,假设有20层,其中每一层参数引起的分布的微小变化迭加起来是巨大的。可以拿方言随距离演变的例子帮助理解:相邻城市之间的方言的差异基本很小,例如北京话和天津话;距离逐渐增大会导致方言逐渐变化,当距离很大时,方言之间的差异也会变得很大,例如北京话和广州话。
接下来自然就引入了BN(Batch Normalization)的概念,即对每一层的输入都作归一化(Normalization),但除此之外还有一些别的操作,公式可以给出最精准的描述:
公式 2 - 4描述了如何在一个batch内计算每一层的均值,标准差,之后减均值,除以标准差,将分布转换为均值为0,标准差为1的标准分布。公式5是BN中最重要的部分,其中γ和β是BN层中的参数,经过公式5后,分布的均值为变为β,标准差为γ。整体上看,BN层的作用就是通过参数控制了每一层输出的均值和标准差。且在特定条件下,BN层有能力恢复输出的原始分布。
1.3 BN没有解决ICS问题
ICS问题是训练过程中,网络中间层输入分布的变化。BN其实并没有解决ICS问题,而是引入了参数γ和β去调节中间层输出的均值和标准差,γ和β会在训练过程中不断更新,意味着均值和标准差也在不断变化,即BN本质上暗含了ICS。从反证法的角度来说,假设BN解决了ICS问题,那么参数γ和β是没有意义的。
既然BN没有解决ICS问题,那它为什么有用呢?!GAN的发明者Ian Goodfellow给了一个可能的解释:神经网络的训练过程中,更新了某一层的权重参数,后续每一层网络的输出都可能发生变化,最终引起loss值的变化。所以当没有BN层时,loss的收敛就需要我们精心设计权重的初始化方法和超参数的调节方法以及等待漫长的训练时间;但当我们在各层之间加入了BN层后,某层的输出仅由两个参数γ和β决定,使用梯度下降法优化参数时,优化方法只需要调节两个参数的值来控制各层的输出,而不需要调节各层的全部参数。这样极大地提高了收敛速度,避免了小心翼翼的参数初始化和超参数调节过程。
1.4 网络使用BN层时需要注意的细节
- 将BN层放在激活层之后:尽管BN的原论文将BN层放在了激活层之前,但实际上,将BN层放在激活层之后有更好的效果。直观上理解似乎也是这样:如果将BN层放在激活层之前,那么BN层的输出还需要经过激活层才能到达下一层,这样BN层就无法完全控制下一层的输入分布;将BN层放在激活层之后就不会有这样的问题。
- 假如推理过程没有batch怎么办?推理过程没有batch(batch_size =1)是很常见的,计算机视觉中一次可能只对一张图片作目标检测。但此时我们又需要计算均值和标准差,用于上述公式4和5计算BN层的输出。主流深度学习的解决方法都是:在训练时跟踪记录每一个batch的均值和标准差,并使用这些值对全部样本的均值和标准差作无偏估计,计算公式见下图:关于标准差的无偏估计在这里就不展开了。值得注意的是:Pytorch中,model.eval()的两个作用,其中之一就在这里,而另一个作用是修正Dropout引起的神经元数值变化。
3. BN层的正则化作用:在BN层中,每个batch计算得到的均值和标准差是对于全局均值和标准差的近似估计,这为我们最优解的搜索引入了随机性,从而起到了正则化的作用。
4.BN的缺陷:带有BN层的网络错误率会随着batch_size的减小而迅速增大,当我们硬件条件受限不得不使用较小的batch_size时,网络的效果会大打折扣。下文中介绍的LN,IN,GN就是为了解决该问题而提出的。2. LN(Layer Normalization),IN(Instance Normalization),GN(Group Normalization)是什么?
2.1 LN,IN,GN的定义
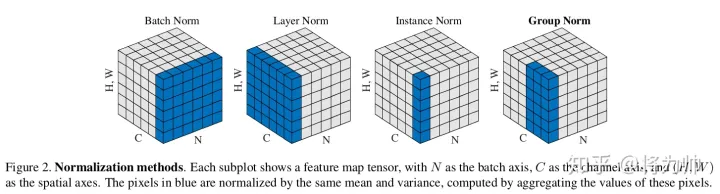
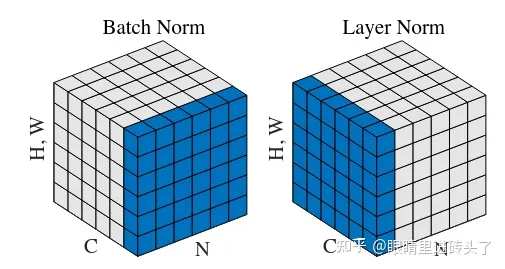
先来张图直观感受下BN,LN,IN,GN的区别与联系:
这张图与我们平常看到的feature maps有些不同,立方体的3个维度为别为batch/ channel/ HW,而我们常见的feature maps中,3个维度分别为channel/ H/ W,没有batch。分析上图可知:BN计算均值和标准差时,固定channel(在一个channel内),对HW和batch作平均;LN计算均值和标准差时,固定batch(在一个batch内),对HW和channel作平均;IN计算均值和标准差时,同时固定channel和batch(在一个batch内中的一个channel内),对HW作平均;GN计算均值和标准差时,固定batch且对channel作分组(在一个batch内对channel作分组),在分组内对HW作平均。更精确的公式描述请大家自行看原论文Group Normalization吧。
可以看到与BN不同,LN/IN和GN都没有对batch作平均,所以当batch变化时,网络的错误率不会有明显变化。但论文的实验显示:LN和IN 在时间序列模型(RNN/LSTM)和生成模型(GAN)上有很好的效果,而GN在视觉模型上表现更好。
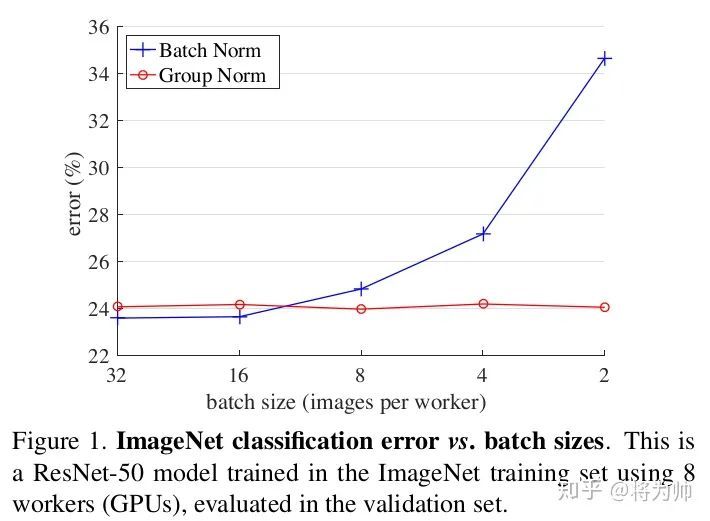
2.2 BN与GN在ImageNet上的效果对比
BN和GN错误率随batch size的变化,BN的错误率随batch size的减小迅速增大,而GN的错误率基本不变 目录:
1.总体看:LN与BN不同在哪?
2.细节点看:BatchNormalization & LayerNormalization
3.为什么做Normalization?
4.CLN(Conditional Layer-Normalization)
5.总结一下,在LN与BN中,可以看到图像中经常用BN, 而NLP中经常用LN,那为什么呢?1.总体看:LN与BN不同在哪?
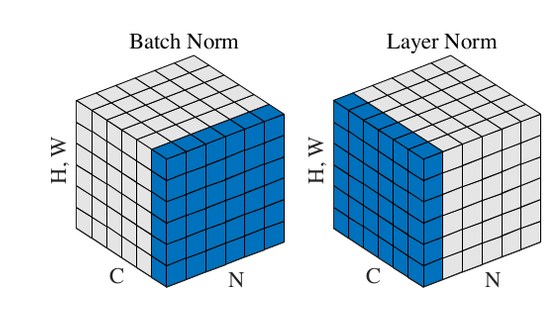
经常会看见讲BN,LN出现这张图,这张图中(N, C, H)就是代表NLP中(batch, seq_len, dim) 。
BN与LN主要区别是,BN针对的是batch内不同样本的同一个特征进行归一化,而LN取的是同一个样本的不同特征进行归一化。
举个例子,在NLP中data shape=[batch, seq_len, dim];
1. BN就是取[batch, 1, dim] 这个切面,计算这个切面的 , 在此切面中每次取[batch, dim=1]作为一个向量进行normalize, 一个向量就是下面BN公式图中B={x1, ... xm}的x1。
2. LN就是取[1, seq_len, dim]这个切面;计算这个切面的 , 在此切面中每次取[seq_len=1, dim]作为一个向量进行normalize.2.细节点看:BatchNormalization & LayerNormalization
其中 就是表示一个样本,一个mini-batch共有m个样本,以上是batch normalization 的公式,前三步是标准的normalization 工序, 第四步还有一个带参数的反向操作, 表示将 经过normalize 后的数据再扩展和平移。
为什么进行正常normalize后又加两参数进行扩展平移?这是为了让模型在训练过程,自适应的去学这个扩展参数 gamma, 和 平移参数 β。这样下来当前面标准化normalize后起到了优化模型结果的作用时,那gamma, β可以进一步加强这种效果,而当标准化normalize没起到作用, 那gamma 和 belt也能自适应的进行调整。
LayerNormalization与BatchNormalization差不多, 就是进行normalize的维度不一致。
其中 表示一个特征,共有H个特征(dim=H),所以LN就是对一个样本做normalization, 而BN是对一个batch的样本同一特征上做normalization,也就是大家常说的横向与纵向上做normalization。
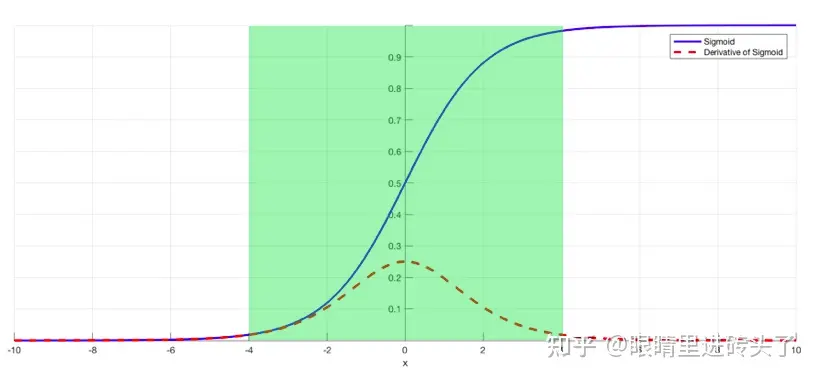
3.为什么做Normalization?
一般Normalization都是在放入激活函数前,Normalization发挥的主要的作用,是为了让数据都尽量分布在激活函数的导数的线性区,避免在落在饱和区,从而避免梯度消失, 也就是下图的绿色区域。
在BN和LN都能使用的场景中,一般优先使用BN,原因是基于不同样本的同一特征进行归一化更不容易损失信息,效果会优于LN。但由于NLP数据的长度不一致,会有padding操作,LN取的是同一个样本与其他样本无关,所以LN会更多出现。
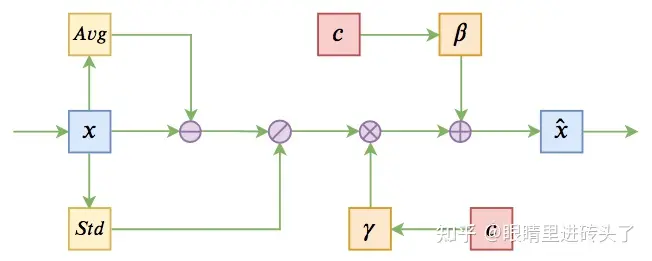
4.CLN(Conditional Layer-Normalization)
结合图(基于Conditional Layer Normalization的条件文本生成)与公式看,g,b就是 ,而c可以认为是模型的输入,即这里认为预先产生的条件, CLN就是在LN的基础上,将输入作为条件融入LN的 ,如参数中,举个例子,假设现在有个任务为看图说话,则条件为图像的embedding,w*c就是将条件输入转成与gama, beta相同的维度进行叠加, 其他的仍然是LN的正常步骤。
5.总结一下
在LN与BN中,可以看到图像中经常用BN, 而NLP中经常用LN,那为什么呢?
一部分原因是文本为变长时序序列,一个batch内存在长短不定问题,这种情况下,BN是没法得到一个稳定的统计量( )。但其实图像中有模型也是有用LN的,如VIT。而在Transformer结构中,都是用的LN。
关于这一点可能得结合Transformer文章中的Scale-Dot Self Attention,文章中就提到为什么进行scale, 就是因为dot-product,当dim大时,q×k(dot-product)造成的梯度更大,导致经过softmax后产生的gradient就很小了,后续与v运算时,self-attention的差异就小了, 所以要进行scale一下。而LN刚好就是在一个向量内进行normalization, 这样就能更有效控制q,k的大小了,从而减缓上面这种情况了。当然了以上只是臆测的,至于作者是不是真这么想的,他没说俺也不知道,瞎聊了几句。
参考:
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- Layer Normalization
- Group Normalization
- 基于Conditional Layer Normalization的条件文本生成
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=1228

Best Last Month
.jpg)
Mechanical electromechanical by wittx

Water conservancy and hydropower by wittxNew MIT Solar-Powered System Efficiently Extracts Drinkable Water From “Dry” Air
Information industry by wittx
Information industry by show

Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittx

Information industry by wittx

Information industry by wittx