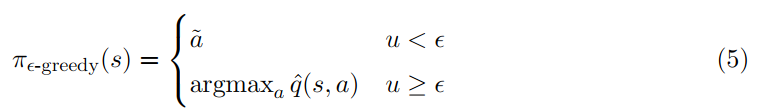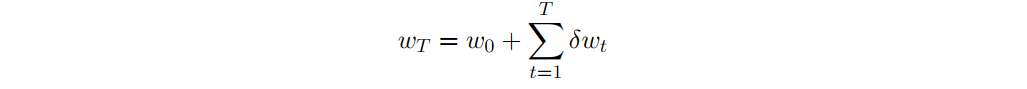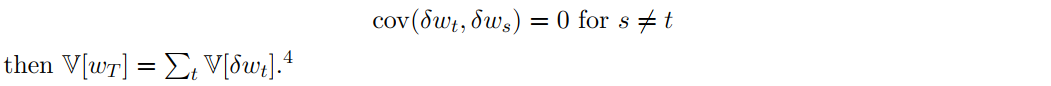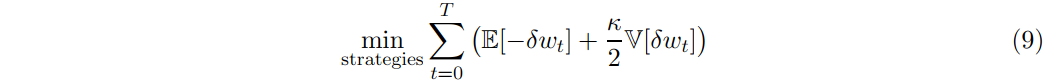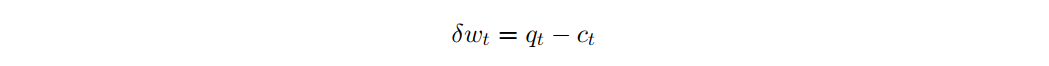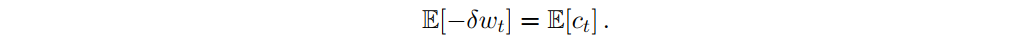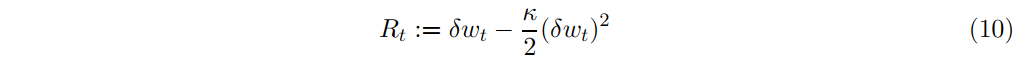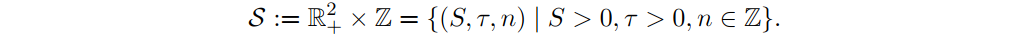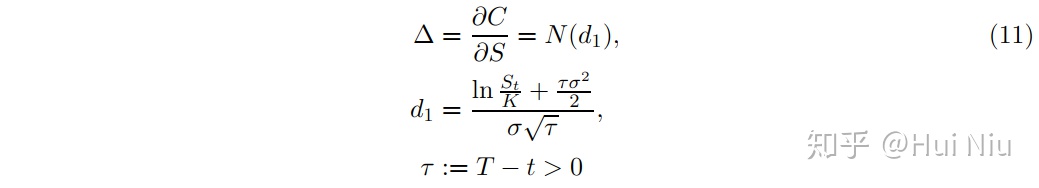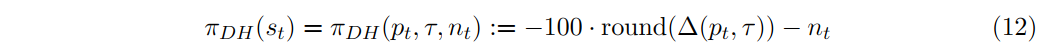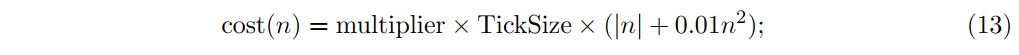- Investment
- 科学论坛
-
Program
News Message
强化学习在期货风险控制
- by wittx 2022-11-23
Dynamic Replication and Hedging: A Reinforcement Learning Approach.
One-Page Review
Summary: Key idea in a sentence or two.
The paper proposed a Reinforcement Learning approach to hedge options in the frictional market(discrete time, trading cost ), providing a trade-off between the trading cost and the replication error.
All it needs is a good simulator of the market (including stock price dynamics, option prices and trading costs). No assumption was made in the stock price model and trading costs.
Learning from critical reading: any problems?
- Poor data efficiency. It is difficult to have a good simulator, especially a good option pricing model.
- Why not just set solid frequency of hedging?No experiment was done to show the result.
Learning from creative reading: idea for next year's conference?
1. Can we use meta reinforcement learning to improve the data efficiency?
2. Consider distributional RL methods.
3. A more complex model. Refer to QLBS.
opinion: Do you recommend this paper?
- Recommend.
以上是我的review,如有不足之处大家可以在评论区补充和讨论。
问题
BSM(Black-Scholes model)中期权的连续复制是不现实的,也会带来无限的交易手续费。现实情况下的期权策略应该是离散的时间和有摩擦的市场。这样的话,期权的对冲策略就取决于它在replication error和trading cost之间的平衡上。(复制的太频繁会比较精确但是会引起比较高的手续费)也就是agent选择的hedging策略取决于它的风险厌恶程度(risk aversion)。
投资组合的再平衡策略必须在离散时间和存在摩擦的市场中完成。在有摩擦的市场中,流动性得不到保证,如果管理不当,对冲的市场影响可能相当大。单只股票的大额交易执行是一个多周期规划问题,可以通过均值-方差优化来解决。期权对冲问题与此类似,但更为复杂。在大多数情况下,对冲本身不是静态的,而是需要不断调整的。尽管如此,这两个问题在某种意义上是相关的,即人们希望最小化(1)交易成本(2)与最优对冲的偏差。
本文提出了一个用强化学习方法来进行对冲的策略。该方法需要有一个很好的市场模拟器来用作环境,能够模拟股价的变化,期权价格,以及市场手续费。但是这些信息是不需要直接给agent的,而是生成环境让agent与之交互。注意这篇文章主要是给出已经持有期权的时候的对冲策略,而不是给期权定价。相反,训练算法需要的模拟器需要有一个比较可靠的期权定价模型。核心想法就是其RL目标函数是一个均值-方差形式,用以权衡对冲频率和对冲精确度。
文章说他们给出的方法有以下贡献:
首先,该方法很general。只要我们知道如何定价衍生证券(即使这个定价是由蒙特卡罗完成的),我们的方法将很快产生一个代理给出如何最优地平衡交易成本和该证券的对冲方差。成本与方差的相对重要性由代理的风险规避参数决定。(也就是说模拟器要很好的模拟期权价格,所以这篇文章不是为了定价,而是为了解决对冲问题。)
第二,方法基于强化学习(RL)。虽然强化学习本身是众所周知的,但这种机器学习技术以前还没有应用于受非线性交易成本影响的离散复制和对冲。值得注意的是,由于本文中提供的技术的灵活性,可以直接加一些feature和一些约束(如循环和仓位约束)来扩展模型。虽然QLBS(halperin2017)将强化学习应用于期权,但是其中的方法对于BSM模型要求的非常具体且不考虑交易成本,而本文方法允许用户“插入”任何期权定价和仿真库,然后无需进一步修改就可以训练系统。文章也与buehler2018deep有关,他们评估基于神经网络的hedging在凸风险度量下的比例交易成本。
第三,该方法是基于一个连续的状态空间,训练既不使用有限状态空间方法,也不要求选择基函数。相反,文章将介绍一种以前从未应用于衍生品对冲问题的训练方法。我们的训练方法依赖于“sarsa target”,并应用一些非线性回归技术。
第四,该方法以一种直接的方式扩展到任意衍生证券投资组合。例如,设想一名交易员继承了一种衍生证券,由于某种外部约束,他们必须持有该证券直至到期。交易员对衍生品或其基础产品没有方向性看法。根据本文提出的方法,交易员实际上可以“按下按钮”来训练一种算法来对冲头寸。然后,该算法可以处理对冲交易,直到到期,不再需要人工干预。
下面我们具体讲一下他们的方法。
用模拟数据和批处理训练
这一节先说一下他们使用的算法框架和实现方式,后面再讲问题的建模。
算法就是使用普通的RL方法sarsa,其中behavior policy是 .
Sarsa:
训练过程:
首先我们定义一个 对的collection batch,其中 是一对state-action pair, 是相应的更新目标(6)。
假设我们要运行B个不同的batch b=1,....,B,我们假设使用每个batch的所有样本,可以用一个非线性回归learner可学习到函数 。合适的非线性回归learner是统计学习文献中经常研究的,它们包括随机森林、高斯过程回归、支持向量回归和人工神经网络。
学到的 再取均值来提高模型的 函数的精度。然后生成第b + 1个batch,使用更新后的 计算 并重复,直到我们有B个batch, 已经更新B次。在用 生成batch和拟合 之间不断交替,直到达到某种收敛准则。本文的模拟使用了B = 5个批,每个批包含75万个 对。
自动对冲
这一节我们介绍问题的理论模型,给出优化目标和reward function。也是文章比较关键的部分。
我们将 automatic hedging定义为使用训练的RL代理来处理特定衍生品头寸的hedging。代理拥有不能交易的多头期权头寸,代理只允许交易用于复制的任何其他非期权头寸。在一个没有交易摩擦的世界里,在一个可以持续交易的世界里,可能存在一个动态复制的投资组合,它可以完美地对冲期权头寸;这意味着整个投资组合(期权减去复制组合)的方差为零。在本文中,我们将考虑摩擦和只有离散交易可能的情况。这里的目标是最小化方差和成本。
假设我们的代理具有二次效用(quadratic utility),我们将推导出奖励函数的精确形式。代理的最佳投资组合是由解决均值-方差最优化问题,风险厌恶系数K:
这里final wealth 是指最后的财富值,可以看做是每时每刻财富值变化δwt的和,即
这样再来看公式(8)的均指项,我们有 。而方差项中,有cross variance 。
但是如果我们假设 随时间增长的独立性,也就是说,
在完全市场中,期权是多余的工具(redundant)。它们可以被连续时间动态交易策略精确复制(方差为零),该策略以无穷小的增量无限频繁地进行交易。在现实世界中,期权的损益方差减去其抵消复制投资组合不为零。参考文献almgren2001optimal,我们的对冲代理想要解决(8)的一个简化版本,即
最小值是在所有允许的交易策略中计算出来的。与almgren2001optimal相比,这里的不同之处在于,机器将通过模拟金融市场并将RL应用于模拟结果来学习最优策略。
如果每日价格过程是一个随机游走,那么 的增量可以分解为(请大家思考为什么可以这么分解?期权价减去股价是随机游走吗?)
其中 为随机游走, 为t期支付的交易总成本(包括佣金、买卖价差成本、市场影响成本及其他滑脱来源)。随机游走的情况下,期望财富增量是期望cost的- 1倍。
换句话说,在这种情况下,问题(9)变成了成本与方差之间的权衡。代理可以更频繁地进行对冲,以减少被套期头寸的方差,但增加了交易成本。
如ritter2017machine所示,通过选择适当的奖励函数,可以将 (期望效用)最大化问题转化为一个RL问题。对应于(9)的每个时段的reward约为
通过将每个单周期报酬代入累积报酬(1),我们得到了均值-方差目标的近似值。因此,用这种奖励函数训练强化型学习者相当于训练期望效用最大化者。在期权对冲的背景下,它相当于训练自动对冲,使他们能够在成本与对冲方差之间进行最优权衡。
实验结果
我们来看一个可能的最简单例子:执行价格为K、到期日为T的非派息股票的欧式看涨期权。我们认为strike和到期日是固定的常数。为简单起见,我们假设无风险利率为零。我们训练的agent将学会用这种罢工和到期来对冲这个特定的选择。它没有被训练来对冲任何可能的罢工/到期的期权。
代理以L个合同的固定期权头寸进入当期。为了简单起见,我们假设这个期权头寸将保持不变,直到期权被行使或到期——我们正在训练一个代理成为一个给定合约的最对冲者,而不是一个可以决定不持有合约的代理。
每个时刻,代理观察一个新的状态,可以决定一个动作。
Action Space
可用的操作总是包括交易基础股票,其界限由问题的经济状况决定。 例如,对于每100股的L合约,人们不希望交易超过100·L股。如果期权是美式,那么还有一个额外的操作,即行使期权,从而以执行价格K买进或卖出股票。、
State Space
在任何成功的RL应用中,状态必须包含与做出最优决策相关的所有信息。不需要包括与任务无关的信息,或者可以直接从状态的其他变量导出的信息。欧式期权中,状态必须至少包含潜在的当前价格St和剩余到期时间τ:= T−t>0,以及我们目前持有股票头寸n。因此,状态:
如果是美式期权,那么在除息日期之前提前行使可能是最佳选择。在这种情况下,状态必须增加一个额外的变量,即t + 1期的预期股息大小。
从业人员通常使用BSM公式计算期权头寸的增量,以达到对冲的目的
但 用隐含波动率取而代之。这被称为delta。注意K和 等参数不提供给代理,尽管它们用于构建代理的模拟训练。如前面第2节所述,agent将通过对随机世界的大量模拟来了解它所在的随机世界的特性。如(11)中给出的∆(S)这样的非线性函数,只要它们影响到最优策略,就会成为agent学习值函数(2)的一部分。
无摩擦市场实验结果
我们模拟了一个BSM世界,但是经过了修改以反映交易的现实: 离散时间和空间。我们考虑一个股票的价格过程是一个几何布朗运动(GBM),初始价格 ,日常对数正态波动率 /天。我们考虑一个初始金额为欧洲看涨期权( ),到期日为 天。我们每天用 个离散时间,因此每个“episode”有 个时刻。我们要求交易量(因此也包括持股量)是股票的整数。我们假设我们的代理的工作是对冲该期权的一份合同。在下面的例子中,参数 。此外,我们设置了风险规避, 。
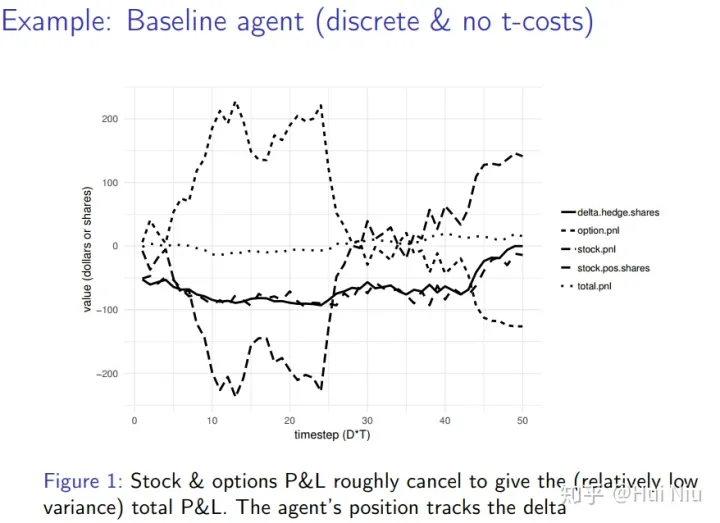
我们首先考虑一个没有交易成本的“无摩擦”世界,然后回答这样一个问题:算法是否可能学习动态复制投资组合策略?算法只能通过观察和与模拟互动来学习。结果如图1所示。
最初,RL代理处于不利地位。回想一下,它不知道任何相关的信息如下:
(1)执行价K,(2)股票价格过程是一个GBM,(3)价格运动的波动性,(4)BSM公式,(5)到期日的回报函数(S−K) +,(6)任何Greeks。
它必须通过与模拟环境的交互,从这些变量中推断出相关信息,只要这些信息影响了值函数。
GBM的每一个样本外模拟都是不同的,但是我们在图1中展示了训练后的一个典型例子。
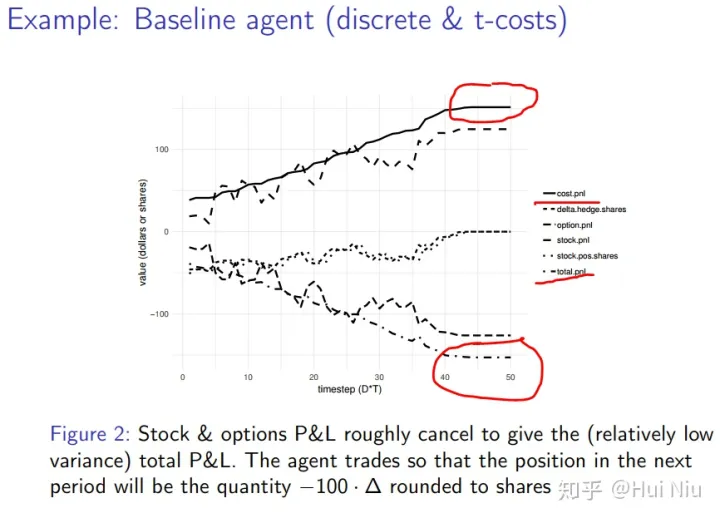
图1。训练后的代理的样本外模拟。我们描述累计股票、期权和总损益(P&L:profit and loss);RL代理在股票中的仓位(stock.pos.shares),以及−100·∆(delta.hedge.shares)。观察到(a)累计股票和期权损益粗略地相互抵消,以给出(相对较低的方差)总损益;(b)即使没有提供delta,RL代理的头寸也会跟踪delta头寸 如图1的例子是在无摩擦的模拟中产生的,为什么总损益不完全为零?这是由于离散化误差造成的。时间是离散的(每天五个时间段),所以连续的对冲是不可能的。此外,该模拟要求交易的股票数量为整数,这又引入了进一步的离散化误差。
Baseline
任何复杂的模型都应该以更简单的模型为基准进行测试。为了证明其额外的复杂性,更复杂的模型应该能够做一些简单的模型不能做的事情。我们定义一个简单的策略, 作为RL所学到的更复杂的策略的baseline。
在公式11中令 记作剩余到期 价格为 时的delta,状态为 , 为当前对冲持有的股票。我们的简单baseline策略必须输出一个动作,即给定这个状态向量要交易的股票数量。定义
其中,round函数返回与参数最接近的整数。
有摩擦市场的实验结果
我们假设有如下的成本函数,自变量是交易股数n。
取TickSize = 0.1,在乘数multiplier = 1的情况下,TickSize×|n|这一项表示相对于中间点的成本,即跨越两个tick宽的买卖价差的成本。(13)中的二次项是市场影响的一个简单模型。图1的乘数为0。
RL方法的一个关键优点是它没有对成本函数的形式(13)做任何假设; 它将学会优化预期效用,无论你提供什么成本函数。在图1中,我们取无摩擦的函数代价中的乘数= 0。我们现在让乘数等于5,代表高度的摩擦。
high-trading-cost环境中我们的直觉是,(如果被对冲的仓位相对于市场的典型的交易量是一个非常大的仓位,这将永远是这样),简单的策略 会交易得太多次了。我们也许可以节省大量的成本,代价是对冲误差的轻微增加。
给定(9)中的均值-方差效用函数,我们期望RL学习方差和成本之间的权衡。换句话说,我们期望它比πDH实现更低的成本,可能未来为代价更高的方差,当平均数量足够大的样本外模拟(即没有以任何方式在训练阶段使用的仿真模拟)。
我们对agent进行了5批训练,每批15000个episode,每个episode有D·T = 50个时间步。这意味着每次对非线性回归学习器的调用都涉及75万对 。训练过程在一个CPU上花了一个小时。在训练之后,我们运行了 个样本模拟。利用样本外模拟,我们在baseline代理和RL代理之间进行了一场比赛,baseline代理只使用delta对冲而忽略成本,而RL代理则用一些成本来换取实现的波动性。
图2显示了baseline代理的一个有代表性的样本外路径。我们看到它过度交易,付出了太多的代价。
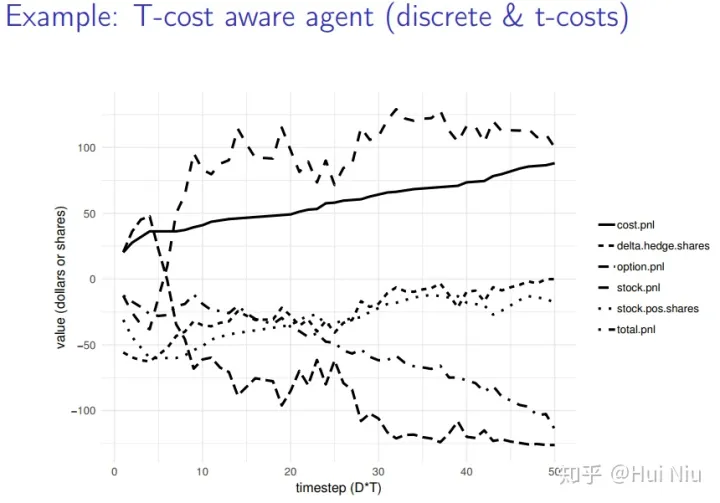
图2,样本外的模拟一个baseline策略πDH。 我们显示累积的股票损益表和期权损益,两者大致相互抵消,从而给出(相对较低的方差)总损益表。 我们用股票表示代理的仓位(stock.pos.shares)。 代理进行交易,使下一个周期的仓位为数量- 100·∆,四舍五入为股份。 图3显示了同一路径上的RL代理。我们看到,在保持对冲的同时,RL代理以一种成本意识的方式进行交易。图3中的曲线代表了代理的仓位(stock.pos.shares),比−100·∆(delta.hedge)的值平滑得多,随着GBM进程自然波动。
图3。 我们训练的RL代理的样本外模拟。 代表对冲仓位(stock.pos.shares)的曲线控制着交易成本,因此比−100·∆(称为delta.hedge.shares)的值要平滑得多,后者自然会随着GBM的进程而波动。 图3只包含一个从样本外的N = 10,000路径集合运行的代表。为了总结所有运行的结果,我们计算了每条路径的总成本和总损益的标准估计。图4显示了所有路径的总成本和总损益的波动率的核密度估计(基本上是平滑直方图)。在每一种情况下,我们执行Welch双样本t检验,看看是否有显著的差异。
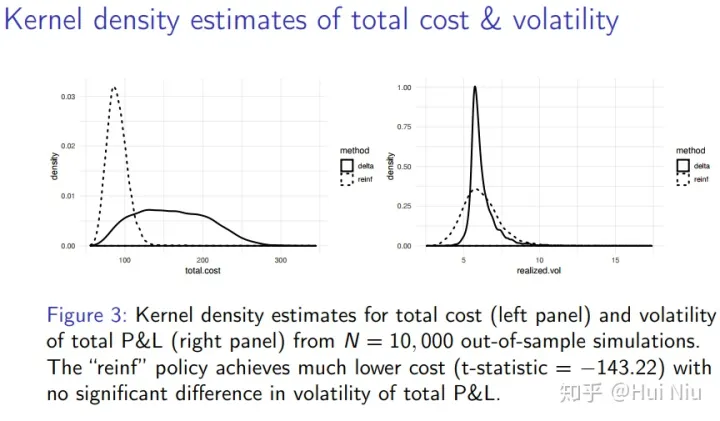
平均成本的差异具有高度统计学意义,t统计量为−143.22。另一方面,vols的差异在99%的水平(.ge.shares)上没有统计学上的显著性,这个水平随着GBM的进程自然波动。
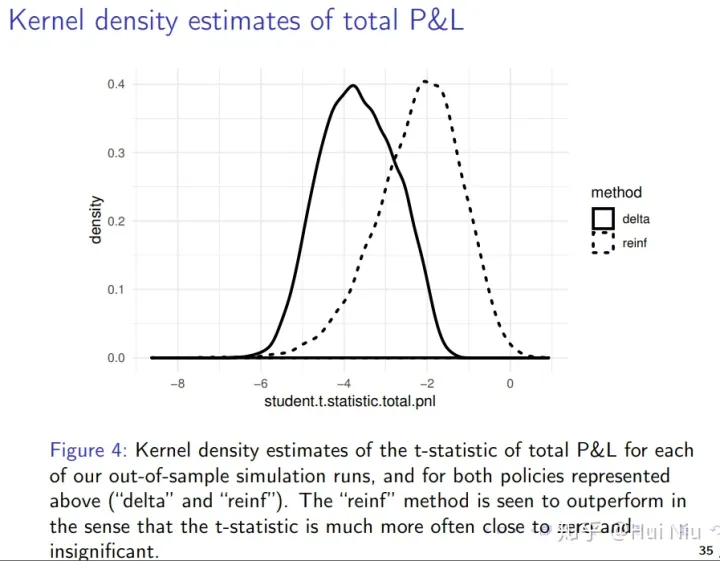
图4。 核密度估计总成本(左面板)和总损益波动率(右面板)从N = 10,000个样本外模拟。 “reinf”政策的成本要低得多(t-statistic =−143.22),且总损益的波动性没有显著差异。 我们还可以通过总损益(包括对冲和所有成本)显著小于零的频率来衡量自动对冲模型的有效性。对于这两种策略(“delta”和“reinf”),我们计算了每次样本外模拟运行的总损益的t统计值,并构建了内核密度估计,见图5。“reinf”方法被认为表现更好,因为它的t统计量更经常接近于零且不显著。
展示5。 对每次样本外模拟运行的总损益的t统计量的内核密度估计,以及对上述两种策略(“delta”和“reinf”)的估计。 “reinf”方法被认为比t统计量更接近于零和无关紧要。 结论
本文的主要贡献是说明使用强化学习(RL)可以训练一个机器学习算法来在现实条件下对冲期权。
有些值得注意的是,它没有来实现用户提供下列信息:(1)执行价K,(2)股票价格过程,日股日经指数不算在内(3)价格的过程,(4)Black-Scholes-Merton (BSM)公式(5)回报函数(S−K) +到期,和(6)的greeks。
RL方法的一个关键优点是它不对交易成本的形式做任何假设。根据交易成本函数,RL学习最小方差的对冲。它所需要的只是一个好的模拟器,在这个模拟器中,交易成本和期权价格可以被精确地模拟出来。
这有一个有趣的含义,即任何可以定价的期权也可以对冲,不管定价是否通过明确地构造一个复制投资组合来完成——不管复制投资组合是否存在于可交易资产类别中。
我们的方法不依赖于完美动态复制的存在。它将学会最优地权衡方差和成本,尽可能最好地使用被赋予作为对冲投资组合中潜在候选资产的任何资产。换句话说,它将找到最小方差动态对冲策略,无论最小方差是否实际上为零(在衍生品定价中通常是这样的,在衍生品定价中,为了获得无套利价格,需要完全复制)。这一点很重要,因为在许多现实情况下,市场是不完整的,因此完美复制所需的一些资产可能不存在。
这种方法的另一个优点是它可以自动处理仓位约束。它是任何RL问题的结构的一部分,对于环境的每个可能状态,代理都有一个(可能依赖于状态的)可能的操作列表。在上面的示例中,可能采取的操作列表是购买或出售最多100股股票(以整数股的数量计算)。我们注意到,其他贸易或头寸限制可以以一种直接的方式纳入,只需修改依赖状态的可用action列表。
在本文中,我们为进一步的研究留下了一些空白。一个明显的兴趣点是在更复杂的硬件上训练像我们这样的代理,从而利用更多的模拟和更精细的时间离散化。silver2017精通描述各种各样的围棋玩家,他们在多达176个gpu和/或48个TPUs的集群上进行训练,训练时间从3天到40天不等。作为参考,本文中的所有示例都是在单个CPU上进行训练的,允许的最长训练时间为1小时。
交易成本不是静态的。交易量的日内结构有一个众所周知的“微笑”形状(由chan1995记录),美国股票交易量的一个重要部分出现在收盘和收盘拍卖中。我们的RL系统应该能很好地处理这类复杂情况。例如,可以用一个微妙的成本函数来扩展模拟器,该函数依赖于每天的时间,并向状态向量添加一个离散的时间指示器。
另一个有趣的研究方向是研究存在交易成本的期权投资组合的最优对冲策略。显然,对于低gamma的投资组合,不需要如此频繁的delta对冲,自然会降低交易成本。一般来说,降低方差的最经济有效的方法可能是使用其他选项,而不是复制投资组合。
文章内容的分享就到这里了,欢迎大家在评论区交流看法。
Reference
[1] Dynamic Replication and Hedging:A Reinforcement Learning Approach. Petter N. Kolm , Gordon Ritter. The Journal of Financial Data Science Jan 2019, 1 (1) 159-171
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=1042

Best Last Month

Information industry by wittx
Information industry by wittx

Information industry by wittx

Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittxFast cycling of lithium metal in solid-state batteries by constriction-susceptible anode materials
.jpg)
Computer software and hardware by wittx
Information industry by wittx
.jpg)
Information industry by wittx